Мозг против теории вероятностей
Однажды ко мне после лекции подошла девушка. Она спросила: «А вы точно борец с мракобесием?» А я ей ответил: «Нет, на самом деле я экстрасенс. Загадайте число от 1 до 20». Девушка загадала число, а я ей говорю: «Вы загадали 8!» Моя собеседница очень удивилась: «Вы что, правда экстрасенс? Как вы угадали?» Я сказал, что настоящие ясновидящие не раскрывают секретов. Но с вами я поделюсь своей тайной: всё дело в том, что это была примерно двадцатая девушка, которая подходила ко мне с подобным вопросом после лекции. Правда, числа предыдущих слушательниц мне не удавалось угадать. И вот наконец «чудо» произошло!
Этот пост – про то, как наш мозг нас обманывает. Начну с простой задачки: представьте, что вы кидаете три шестигранных кубика. Вопрос: что вероятнее – что выпавшие числа в сумме составят 3 или 4? Иными словами, что легче получить – три единицы или две единицы и двойку? Несмотря на то, что люди играли с кубиками с незапамятных времён, ответ на такую задачку удалось найти лишь в XIII веке. Итак, вероятность выпадения четвёрки выше. Почему? Дело в том, что сумме, равной четырём, удовлетворяют три «элементарных события»: двойка может выпасть на первом кубике, на втором или на третьем (при условии, что на двух других единицы). А сумму, равную трём, можно получить только одним способом. То есть вероятность выпадения суммы, равной четырём, в три раза выше. Вроде всё просто! Но решение нашлось относительно недавно.
Всё дело в том, что теория вероятностей ужасно контринтуитивна. Люди часто принимают закономерности за случайные события, а случайные события – за закономерности. И сегодня мы разберём, почему это серьёзная проблема – и как она способствует появлению веры в разные странные вещи – в магию, экстрасенсорику, гадания, общение с духом прабабушки и прочие «чудеса».
«Мой мозг предсказал будущее!»
Расскажу историю про человека по имени Рой Салливан. Этот американец работал инспектором по охране национального парка в Вирджинии. Однажды его ударила молния. Потом молния ударила Салливана ещё раз. И ещё. И снова. И опять. Всего, согласно Книге рекордов Гиннесса, молния поражала несчастного рейнджера семь раз – но он остался в живых (в итоге Рой в возрасте 71 года, по версии следствия, покончил с собой из-за неразделённой любви). Кстати, жену Салливана, которая была младше супруга на 30 лет, тоже ударяла молния – и она выжила.
Удар молнии – не самое частое событие. Может показаться, что история Роя – это что-то невероятное и из ряда вон выходящее. Но на самом деле нельзя забывать, что Салливан работал рейнджером в Вирджинии. В этом штате порядка сорока дней в году – штормовые, то есть вероятность попадания в человека молнии в такое время повышается. Кроме того, Салливан работал на природе – ещё одна дополнительная угроза удара молнией. Но это всё мелочи на фоне самого главного. На планете живут миллиарды людей, и подобная история могла произойти с любым из нас. Случись она не с Роем, а с Ромой, мы бы сейчас обсуждали другого человека. Причём не обязательно должна была случиться история с молнией. Может быть, на Рому пять раз напала бы акула или он попал бы в десять автоаварий. Было бы странно, если бы ни с кем никогда не происходили подобные «чудеса».
Вообще чудо – это маловероятное событие, которое иногда с кем-то происходит – и отнюдь не по воле богов или высших сил. Если определить «чудо» как событие, вероятность которого, скажем, 1 к миллиарду в течении одного дня для одного человека, то ежедневно на планете происходит в среднем 8 чудес. Иногда это называют «Законом действительно больших чисел» (не путать с просто «законом больших чисел» из теории вероятностей): на достаточно большой выборке будут случаться крайне маловероятные события. Всё это усугубляется тем, что именно маловероятные события привлекают наш интерес. Например, иногда люди говорят, что им снятся вещие сны. «Мой мозг предсказал будущее, мой сон сбылся!» – рассказывают они. На самом деле сны людям снятся регулярно, но не все они сбываются. Про несбывшиеся сны мы забываем, а вот про один-единственный сбывшийся помним ещё двадцать лет и всем рассказываем. И снова наша жизнь наполняется «чудесами».
Наш мозг обманывает нас и более изощрёнными способами. Вот попробуйте решить ещё одну задачку: где-то на свете живёт девушка Линда. Ей 31 год, она за словом в карман не лезет и очень сообразительна. Она училась на факультете философии. Студенткой много размышляла о дискриминации и социальной несправедливости, участвовала в демонстрациях против распространения ядерного оружия.[ЕШ1]
Вопрос: что более вероятно?
1. Линда – кассир в банке;
2. Линда – кассир в банке и активная феминистка.
Это задачка на «ошибку конъюнкции», которую сформулировали лауреат Нобелевской премии по экономике Даниэль Канеман и психолог Амос Тверски. Правильный ответ на неё – 1, потому что вероятность совместных событий (Линда и кассир, и феминистка) всегда ниже, чем вероятность одного отдельного события (Линда – просто кассир). Канеман и Тверски заметили, что респонденты чаще всего дают на поставленную задачку неправильный ответ. Да и вообще ошибка конъюнкции, которую также называют проблемой Линды, свойственна большинству людей. Но особенно свойственна она тем, кто верит в разные теории заговора и паранормальные явления.
«От гомеопатии никто особо не умирает»
А теперь поговорим о парадоксе Симпсона – явлении в статистике, которое показывает неправомерность обобщений по нерепрезентативным выборкам. Звучит не очень понятно, поэтому объясню на примере: представьте, что вы читаете научную работу об эффективности гомеопатии. Авторы статьи пригласили для исследования 500 добровольцев, страдающих от опасной болезни. 250 из них лечились гомеопатией, вторая половина – нормальными лекарствами с доказанной эффективностью. В итоге выяснилось, что те пациенты, которые лечились сахарными шариками, выздоравливали чаще! Как такое могло произойти с точки зрения теории вероятностей?
Дело в том, что из 500 человек 300 страдали от лёгкой формы болезни, а остальные – от тяжёлой. Из 300 «лёгких» 200 лечились гомеопатией, а 100 – нормальными лекарствами. За неделю из 100 правильно лечившихся выздоровело 90 пациентов, а из 200 любителей шариков выздоровело лишь 150 (75%). А вот «тяжёлых» чаще лечили нормальными лекарствами: из 200 пациентов 150 принимали таблетки, 50 – гомеопатию. Из 150 лечившихся правильно за неделю выздоровела треть пациентов. А из 50 любителей гомеопатии выздоровело пять человек – всего 10%!
При этом, когда мы «смешиваем» тяжёлых и лёгких пациентов, выясняется, что гомеопатия помогла 155 людям, а лекарства – лишь 140. В общем, возникает парадокс Симпсона – когда при соединении разных массивов данных тенденция исчезает или меняется на противоположную. Этот же парадокс возникает, когда говорят: «От гомеопатии никто особо не умирает, а вот от обычной медицины только так пациенты гибнут». Но гомеопатией обычно не лечат переломы черепа, рак и гнойный перитонит – ей чаще всего лечат простуду. Не стоит манипулировать данными и сравнивать пациентов с насморком, которые и так поправятся через неделю, и пациентов с онкологией.
Кстати, вот недавний пример парадокса Симпсона: в Великобритании в какой-то момент смертность среди привитых от коронавируса стала выше, чем среди непривитых… Граждане забили тревогу: мол, смотрите, прививки убивают людей! Но на самом деле тогда в стране поголовно прививали стариков, инвалидов, пациентов с диабетом и раком. При этом не все здоровые и молодые британцы были привиты. Но антипрививочники, конечно, закрыли на этот факт глаза – и кричали про вред вакцин. Хотя исследователи, которые в той же Великобритании сравнивали привитых и непривитых из одной возрастной группы, выяснили: иммунизация снижает риск смерти.
Некоторые сторонники лженаучных идей иногда специально пользуются тем, что люди плохо ладят с теорией вероятностей. В той же Великобритании живёт парапсихолог Руперт Шелдрейк, автор книги «7 экспериментов, которые изменят мир». Руперт создал целый «научный метод» для доказательства экстрасенсорных способностей. Но секрет метода заключается в том, что Шелдрейк специально вносил в экспериментальные протоколы ошибки, которых наука пытается избежать. Это ошибки наподобие парадокса Симпсона — разные трюки при обработке данных, которые дают невероятные результаты.
Вот один из экспериментов, который описал парапсихолог. В нём участвовал человек с фантомной рукой (то есть человек, который лишился конечности, но по-прежнему её чувствовал). Доброволец должен был «положить» свою руку на одно из двух мест. При этом приглашённый экстрасенс пытался почувствовать, где же эта рука находится. Шелдрейк пишет: сначала маги не очень угадывали, где именно находится конечность, но со временем количество правильных ответов начало расти. «Значит, экстрасенсы чувствуют ауру тела!» -- пришёл к выводу мужчина. Можете сами повторить такой эксперимент и опровергнуть проклятую материалистическую науку! При это Шелдрейк описывает два важных условия, чтобы эксперимент с работал. Во-первых, «экстрасенсам» каждый раз надо сообщать, угадали они или нет. А, во-вторых, нельзя доверять управление фантомной рукой генератору случайных чисел, добровольцы должны сами решать, когда и как им руку двигать.
В чём тут фокус? Когда люди пытаются имитировать случайность, у них, как правило, не очень получается. Психолог Питер Брюгер обнаружил эффект «избегания повторений»: имитируя случайные броски кубика, человек будет стараться не называть шестёрку после шестёрки, пятёрку после пятёрки и так далее, хотя на самом деле вероятность выпадения того или иного значения от предыдущего броска не зависит. Причём этот эффект особенно сильно выражен у верующих в паранормальное, в меньшей степени у агностиков и в ещё меньшей у скептиков.
Поэтому и в эксперименте Шелдрейка человек с фантомной конечностью не будет двигать ей случайно, даже если захочет, а будет следовать неким собственным представлениям о вероятных паттернах. Если экстрасенсу каждый раз сообщать, прав он или ошибся, вскоре он начнёт «предсказывать» поведение добровольца, угадывать эти паттерны, делать похожие не случайные выборы. Вот и весь секрет. Шелдрейк сумел воспроизвести в реальном мире известную шутку математиков: «Генерация случайных чисел слишком важна, чтобы оставлять её на волю случая!»
«Так, бабушка велела передать тебе: не надо ссориться из-за денег!»
Во многих компьютерных играх, где есть элементы случайности, разработчики специально придумывают «кармические кубики». Например, в «Baldur’s Gate III» игрокам постоянно надо подбрасывать двадцатигранные кубики – выпавшее число влияет на исход беседы, применение заклинания, изучение местности и так далее. Разработчики сделали так, что, если в предыдущий раз у пользователя выпало низкое значение на кубике, в следующий раз шанс успеха повысится (и наоборот) – таким образом у игроков не будет череды одних везений или сплошных неудач. Парадоксально, но подобная «неслучайность» лишь усиливает иллюзию случайности, подгоняя её под наши ожидания. Впрочем, в «Baldur’s Gate III» кармические кубики можно отключить – и тогда числа будут выпадать в соответствии с нормальной статистикой. Кстати, игра очень крутая – рекомендую.
Однажды я очень напугал свою бывшую девушку. Мы играли в такую игру: созванивались по ночам, она воображала какую-нибудь геометрическую фигуру – треугольник, квадрат или круг – а я угадывал, что моя девушка загадала. Я угадывал намного лучше, чем 1/3, предположительно потому, что мы оба избегали «случайных» повторений. Но моя бывшая девушка испугалась мистики и попросила прервать эксперимент.
Нашим плохим знанием теории вероятностей пользуются медиумы и фокусники. Так, в 2020 году вышла статья «Разговариваем с мёртвыми в школьном классе». Её авторы позвали в школу фокусника. Тот пришёл в класс и сделал вид, будто умеет говорить с покойниками. Фокусник называл имя умершего, а по реакции школьников понимал, кому из них мертвец приходится родственником. В итоге 65% подростков поверили, что к ним приходил настоящий медиум. Кстати, «медиумы» так и работают – по возрасту клиентов догадываются (иногда – со второй или третьей попытки), кто у них умер – мама, супруг или ребёнок. А потом говорят: «Так, бабушка велела передать тебе: не надо ссориться из-за денег! А ещё она тебя очень любит даже с того света». И люди такие: «Вау, как он догадался, что мы прямо сейчас делим наследство? Настоящий маг!» Но на самом деле после смерти родственников люди часто ругаются из-за финансов.
При этом после «сеансов» клиенты забывают об ошибках гадалок и медиумов. А вот если экстрасенс что-то угадал – это запоминается. В обычной жизни всё то же самое: мы обращаем внимания на «чудеса» и совпадения и совершенно не помним какие-нибудь несбывшиеся сны.
Приведу ещё один статистический трюк из арсенала «экстрасенсов». Представьте, что вы хотите разбогатеть. Вы можете взять базу людей, которые делают ставки на спорт – и разослать им бесплатные советы, на кого лучше поставить в ближайшем матче или лошадином забеге. Рекомендации вы можете взять из пула случайных исходов. Кому-то ваши советы «помогут» -- дайте этим счастливчикам ещё одни рекомендации на новый матч. Часть любителей ставок ваши советы снова выручат – тогда предложите им очередную консультацию, но уже за деньги. Или за долю от выигрыша. Есть вероятность, что люди согласятся, ведь они сами видели ваши «невероятные способности» на практике. Но на самом деле заниматься такими вещами я не советую – всё-таки деньги стоит зарабатывать честным трудом.
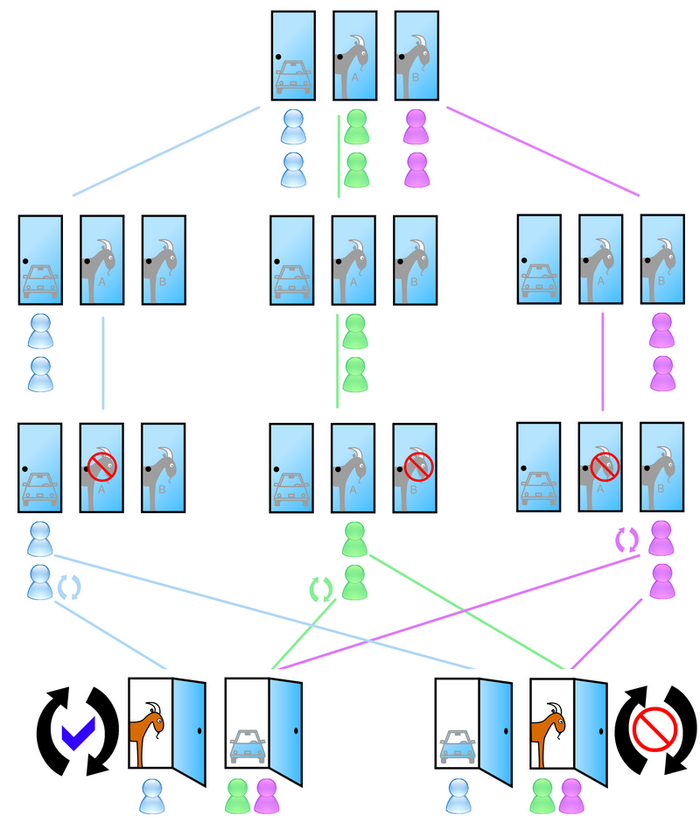
Ещё одна задачка: представьте, что вы попали на Страшный суд. Перед вами – три двери: за одной Рай, за двумя другими — бездна Ада. Когда вы выбрали (но не открыли!) дверь, Архангел, который знает правильный ответ, открывает одну из оставшихся дверей — и это обязательно дверь в Ад. После этого вам дают шанс сменить первоначальный выбор. Вы знаете, что Архангел всегда ведёт себя одинаково и честно. Если что, вы хотите попасть в Рай. Вопрос: что выгоднее — сменить выбор, оставить его прежним, или же разницы нет?
Чаще всего респонденты отвечают, что выбор неважен: шансы угадать нужную дверь в любом случае 50/50. Но оказывается, что, если изменить свой выбор, ваши шансы попасть в Рай повысятся в два раза! Как так? Дело в том, что вероятность отгадать дверь с первого раза — 33%. Поэтому, если не менять выбор, то шанс останется один к трём. Но, если поменять выбор, то шанс вырастает до 66%. Ведь с первого раза вы могли выбрать одну из двух неправильных дверей (шанс 2 к 3), и в обоих случаях попадёте в Рай — вторую неправильную дверь убрал Архангел. И только если вы изначально выбрали Рай, вы проиграете (шанс 1 к 3).
Возможно, у вас внутри всё восстаёт — как может измениться шанс, если я уже сделал выбор? — но объяснение станет гораздо нагляднее, если представить не три, а 1000 дверей. Тогда после вашего случайного выбора наш Архангел любезно убирает не одну, а 998 неправильных дверей. Изначально ваши шансы выбрать Рай были всего 1/1000. А после, если сменить дверь — в 999 случаях та дверь, которую НЕ выбрал Архангел, и ведёт в Рай.
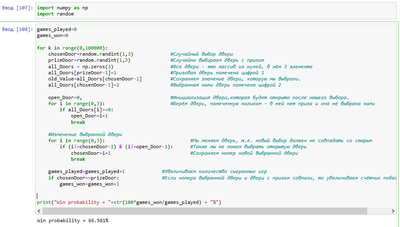
Эта задача всегда вызывает огромный когнитивный диссонанс. Наверняка сейчас в комментариях появятся люди, которые скажут, что всё это чушь, вероятность составляет 1 к 2 и не меняется. Да, теория вероятности – это, повторюсь, очень контринтуитивная штука. А задачка про Гавриила – это вариант известного парадокса Монти Холла, только в оригинале речь шла не о Рае и Аде, а о машине и козах. Можете проверить, что ответ, данный выше, верен экспериментально. Мы с другом в свое время проверяли.
Мораль сегодняшнего поста проста: прежде чем считать что-то чудом, подумайте, не обманывает ли вас мозг. Теория вероятностей уж очень легко сбивает с толку. А если вас заинтересовала тема когнитивных искажений – советую пройти тематический курс, после которого, я уверен, вы больше никому не дадите себя обмануть. Жаль, что такому редко учат в школах.
P.S. Сегодня я предложил вам решить несколько задачек. Напоследок загадаю ещё одну, а ответы на неё пишите в комментариях. Итак, двум заключённым выдали по две монетки и рассадили в две разные башни. Каждый заключённый должен подкинуть свою монетку и угадать, что выпало на монетке товарища по несчастью. Тюремщики обещают, что, если хотя бы один заключённый даст правильный ответ, то обоих мужчин отпустят. В противном случае их обоих казнят. Коммуникация после броска невозможна, повлиять на бросок нельзя, но можно договориться о чём-то до начала испытания. Внимание, вопрос: существует ли способ, с помощью которого заключённые гарантированно выйдут на свободу?




Наука | Научпоп
8.3K постов80.7K подписчиков
Правила сообщества
Основные условия публикации
- Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
- Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
- Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
- Видеоматериалы должны иметь описание.
- Названия должны отражать суть исследования.
- Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
- Посты-ответы также должны самостоятельно (без привязки к оригинальному посту) удовлетворять всем вышеперечисленным условиям.
Не принимаются к публикации
- Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
- Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
- Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
Наказывается баном
- Оскорбления, выраженные лично пользователю или категории пользователей.
- Попытки использовать сообщество для рекламы.
- Фальсификация фактов.
- Многократные попытки публикации материалов, не удовлетворяющих правилам.
- Троллинг, флейм.
- Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает и общество Пикабу.